BLOCS DE FILOSOFIA » septiembre 30, 2019

Canales

22264 temas (22072 sin leer) en 44 canales

Associacions

• Adhoc. Filosofia a secundària (25 sin leer)
• Associació filosófica de les Illes Balears (99 sin leer)

Estudiants

• telèmac (1025 sin leer)

Professors

• A l'ombra de Zadig. (165 sin leer)
• Aprender a Pensar (181 sin leer)
• aprendre a pensar (70 sin leer)
• ÁPEIRON (16 sin leer)
• Blog de Filosofía - Filosóficamente - Blog de Filosofía - Filosóficamente (23 sin leer)
• Boulé (267 sin leer)
• carbonilla (45 sin leer)
• Comunitat Virtual de Filosofia (739 sin leer)
• CONTRA LA NECIESA (31 sin leer)
• CREACIÓ FILOSÒFICA II (28 sin leer)
• DE SOFISTA A SAVI (10 sin leer)
• DIDÁCTICA de la FILOSOFÍA (41 sin leer)
• Educación y filosofía (229 sin leer)
• El café de Ocata (4655 sin leer)
• El club de los filósofos muertos (88 sin leer)
• El Pi de la Filosofia
• EN-RAONAR (489 sin leer)
• ESTÈTICA DE L'EXISTÈNCIA. (570 sin leer)
• Filolaberinto bachillerato (209 sin leer)
• FILOPONTOS (10 sin leer)
• Filosofía para cavernícolas (598 sin leer)
• FILOSOFIA A LES TERMES (164 sin leer)
• Filosofia avui
• FILOSOFIA I NOVES TECNOLOGIES (36 sin leer)
• Filosofia para todos (134 sin leer)
• Filosofia per a joves (11 sin leer)
• L'home que mira (74 sin leer)
• La lechuza de Minerva (26 sin leer)
• La pitxa un lio (9381 sin leer)
• LAS RAMAS DEL ÁRBOL (78 sin leer)
• Materiales para pensar (1017 sin leer)
• Meditacions des de l'esfera (13 sin leer)
• Menja't el coco! (30 sin leer)
• Minervagigia (24 sin leer)
• No només filo (61 sin leer)
• Orelles de burro (498 sin leer)
• SAPERE AUDERE (566 sin leer)
• satiàgraha (25 sin leer)
• UN LUGAR PARA APRENDER FILOSOFÍA (69 sin leer)
• UNA CAIXA D´EINES PER PENSAR (40 sin leer)
• Vida de profesor (212 sin leer)

(3 sin leer)

• septiembre 30, 2019
• 10:33

  El hombre fragmentado

   » ‎ El café de Ocata
  Me he ido alejando de la televisión. Cada vez me interesa menos lo que veo y no creo que sea tanto un problema de los programadores como mío, que todo me suena a visto y revisto. Me pasa casi lo mismo con el cine. Y con buena parte de las novelas que empiezo y que no consigo acabar (hago una excepción notable con las recomendaciones de mi amiga B., que siempre son certeras). Cada vez leo menos libros nuevos y más libros viejos, porque encuentro en ellos posibilidades de pensamiento que han quedado sin desarrollar en el ogulloso presente. Cada vez me interesa más la historia, especialmente tal como la cuentan sus protagonistas porque todos sabemos que es inevitablemente parcial y, por eso mismo, es más honesta. 
  Cada vez tengo más ideas para desarrollar, más libros en proyecto. Así que he de ordenarlos bien en fila. Sin embargo, los proyectos son caprichosos y se mueven por la fila un poco a su antojo, de manera que siempre acabo escribiendo el que no era el primero. Y eso está bien.
  Cada vez creo comprender mejor a Kant, hoy tan denigrado. Me parece que a él no le importaba tanto encontrar un imperativo moral categórico como responder a la pregunta de cómo ser moral de forma no fragmentaria. El imperativo categórico es la respuesta que encuentra a esta pregunta. A su parecer, sólo el deber puede mantenernos unidos a nosotros mismos. Su pregunta es la mía, su respuesta, si hago caso a mis actos, no. Pero pudiera ser que eso que llamamos prudencia sea el intento de ser moral fragmentariamente sin por ello sentir mucha vergüenza.

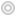• 10:00

  El triángulo cordobés

   » ‎ Aprender a Pensar

  Por Ana Casado, editora del equipo de Matemáticas de SM.

  En el currículo de Secundaria de Andalucía aparece como contenido “el triángulo cordobés”. Pero…, ¿qué es un triángulo cordobés?
  Un triángulo cordobés es un triángulo isósceles cuyos lados están en proporción cordobesa.
  El concepto de proporción cordobesa “surge por casualidad, como feliz resultado de un esplendoroso fracaso” como lo explicaba el arquitecto cordobés Rafael de la Hoz Arderiu,s que descubrió y bautizó así a la proporción numérica 1,3.
  El arquitecto, amante de las matemáticas, inició un proyecto para certificar la proporción áurea* como canon de belleza universal. Su hipótesis era que a lo largo de historia se había utilizado de forma consciente o inconsciente dicha proporción. Eligió Córdoba para llevar a cabo el estudio por ser una ciudad milenaria donde se habían instalado diversas culturas y por ser su ciudad natal. El resultado fue un fracaso y cancelaron el proyecto. Exceptuando algunos casos puntuales de obras diseñadas por arquitectos no cordobeses, no se encontró la ansiada proporción áurea.

  

  Al poco tiempo, la Diputación de Córdoba le pidió preparar un test de aptitud para asignar becas a estudiantes de Arquitectura. Entre las preguntas propuestas, estaba esta:

  “Entre los dos rectángulos siguientes, uno notablemente rechoncho y otro acusadamente alargado (…) tiene que existir un rectángulo equilibrado, bello, perfecto. Dibújenlo”.

  

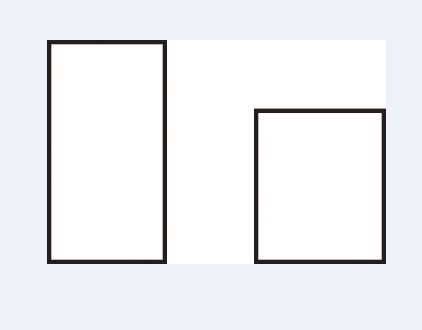
  La calificación máxima a esta pregunta se otorgaba al dibujar el rectángulo áureo. El resultado fue sorprendente porque ningún estudiante dibujó el rectángulo áureo, y una mayoría significativa sí dibujó un rectángulo menos esbelto que cumplía la siguiente proporción:

  

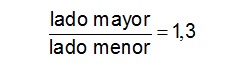
  A partir de este resultado, se comenzó una investigación repitiendo esta pregunta a personas residentes o nacidas en Córdoba. La frecuencia de la proporción 1,3 fue igualmente muy alta. ¿Por qué la preferencia por la proporción cordobesa y no por la proporción áurea considerada ideal de belleza universal?
  Al tener este resultado carácter local, se comenzó estudiando las proporciones de la figura humana en las artes locales cordobesas y se hallaron en el museo arqueológico local, esculturas y mosaicos con figuras humanas proporcionadas según la razón constante 1,3, más próxima al hombre de carne y hueso que al hombre ideal de Leonardo Da Vinci (Studio o El hombre de Vitrubio) o de LeCobusier (El Modulor).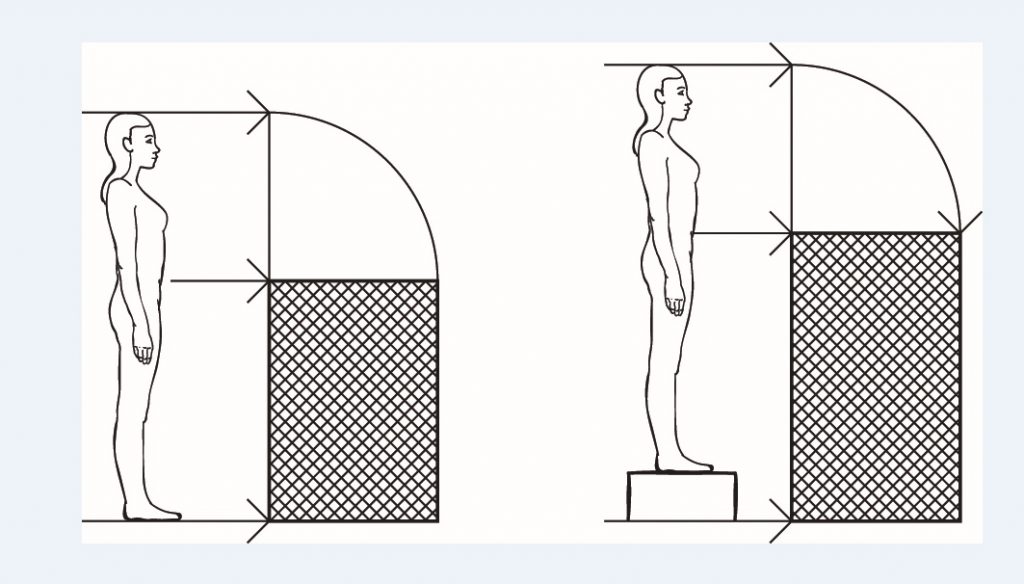

  Proporción humana y proporción divina. Portada de la Mezquita de Córdoba.

  Se retomó el proyecto de analizar las proporciones de la arquitectura cordobesa y se hallaron múltiples ejemplos donde se utiliza esta proporción.

  La portada y las arcadas de la Mezquita, la fachada interior de la Sinagoga, la portada de la casa de D. Juan Cosme de Paniagua, la iglesia de Santa Marina de las Aguas, la fachada del convento franciscano de Capuchinos…

  A lo largo de los siglos, era evidente en Córdoba, la preferencia por esta proporción que el arquitecto Rafael de la Hoz bautizó como proporción cordobesa.
  El siguiente paso fue establecer el origen geométrico de esta razón. Como la proporción áurea se obtiene como la razón entre el radio y el lado de un decágono regular, no fue complicado averiguar que la razón 1,3 correspondía a la proporción entre el radio y el lado de un octógono regular.

  Proporción áurea. 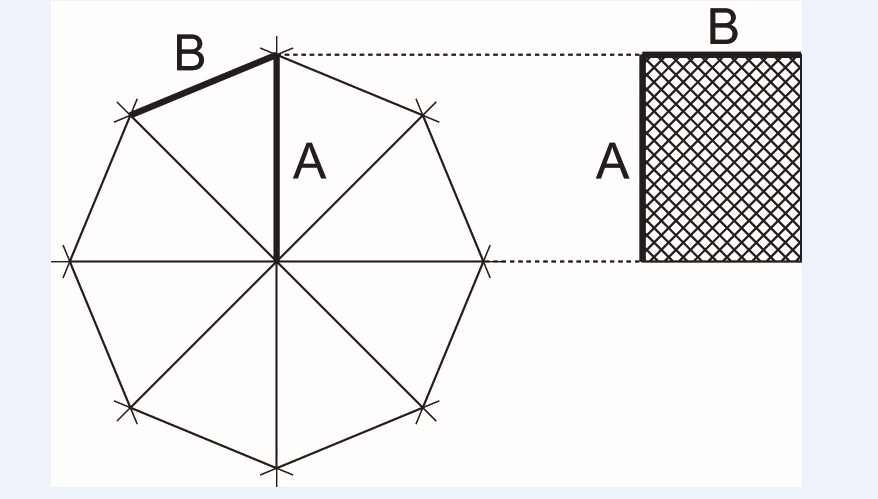Proporción cordobesa.

  El octógono era una figura habitual en la arquitectura cordobesa: las cubiertas de la catedral, las bóvedas de la mezquita, los artesonados de Córdoba y Baena, la plaza de Aguilar, la planta de las torres de la Malmuerta, la fuente del Potro,…

  

  Inicialmente se pensó que la proporción cordobesa tenía carácter local, pero fueron surgiendo estudios que identificaban esta proporción en distintos lugares y épocas. Algunos ejemplos son: las pirámides de Keops, Kefren y Mikerinos, en Egipto, el Panteón de Agripa y la basílica San Pablo Extramuros, en Roma, el arco del Triunfo y el hotel Mayenne, en París,…

  

  La entrada El triángulo cordobés se publicó primero en Aprender a pensar.

• 6:55

  Atzar i teories de la conspiració.

   » ‎ La pitxa un lio
  
  
  
  
  ... necesitamos ubicar los eventos en un contexto emocionalmente entendible, con una clara frontera moral. Algo que anule el azar o la autonomía de los agentes de la ecuación, dándole un sentido unitario.
  
  Pero, si algo hace a la teoría de la conspiración totalmente inexpugnable es su relación con la verdad. Para el profeta de la conjura, la verdad no es algo que deba ser contrastado, sino revelado y denunciado. Así, sólo cuando los ciudadanos caigan del caballo podrán entender el plan que le ocultan los poderosos y del que ellos son meros peones. Y puede que eso no les ayude a saber de la complejidad de las cosas, lo que realmente acontece, pero al menos sí les ayudará a vivir más tranquilos.
  Pablo Simón, Tolstoi y la conspiración, El País 30/09/2019
  [https:]]