Canales
21867 temas (21675 sin leer) en 44 canales
-
 Adhoc. Filosofia a secundària
(25 sin leer)
Adhoc. Filosofia a secundària
(25 sin leer) -
Associació filosófica de les Illes Balears (98 sin leer)
-
 telèmac
(1001 sin leer)
telèmac
(1001 sin leer)
-
 A l'ombra de Zadig.
(160 sin leer)
A l'ombra de Zadig.
(160 sin leer) -
 Aprender a Pensar
(180 sin leer)
Aprender a Pensar
(180 sin leer) -
aprendre a pensar (68 sin leer)
-
ÁPEIRON (16 sin leer)
-
Blog de Filosofía - Filosóficamente - Blog de Filosofía - Filosóficamente (23 sin leer)
-
Boulé (267 sin leer)
-
 carbonilla
(45 sin leer)
carbonilla
(45 sin leer) -
 Comunitat Virtual de Filosofia
(732 sin leer)
Comunitat Virtual de Filosofia
(732 sin leer) -
 CONTRA LA NECIESA
(31 sin leer)
CONTRA LA NECIESA
(31 sin leer) -
CREACIÓ FILOSÒFICA II (28 sin leer)
-
 DE SOFISTA A SAVI
(10 sin leer)
DE SOFISTA A SAVI
(10 sin leer) -
 DIDÁCTICA de la FILOSOFÍA
(41 sin leer)
DIDÁCTICA de la FILOSOFÍA
(41 sin leer) -
 Educación y filosofía
(229 sin leer)
Educación y filosofía
(229 sin leer) -
El café de Ocata (4575 sin leer)
-
El club de los filósofos muertos (88 sin leer)
-
 El Pi de la Filosofia
El Pi de la Filosofia
-
 EN-RAONAR
(489 sin leer)
EN-RAONAR
(489 sin leer) -
ESTÈTICA DE L'EXISTÈNCIA. (570 sin leer)
-
Filolaberinto bachillerato (209 sin leer)
-
FILOPONTOS (10 sin leer)
-
 Filosofía para cavernícolas
(586 sin leer)
Filosofía para cavernícolas
(586 sin leer) -
 FILOSOFIA A LES TERMES
(164 sin leer)
FILOSOFIA A LES TERMES
(164 sin leer) -
Filosofia avui
-
FILOSOFIA I NOVES TECNOLOGIES (36 sin leer)
-
 Filosofia para todos
(134 sin leer)
Filosofia para todos
(134 sin leer) -
 Filosofia per a joves
(11 sin leer)
Filosofia per a joves
(11 sin leer) -
 L'home que mira
(74 sin leer)
L'home que mira
(74 sin leer) -
La lechuza de Minerva (26 sin leer)
-
La pitxa un lio (9230 sin leer)
-
LAS RAMAS DEL ÁRBOL (78 sin leer)
-
 Materiales para pensar
(1015 sin leer)
Materiales para pensar
(1015 sin leer) -
 Meditacions des de l'esfera
(13 sin leer)
Meditacions des de l'esfera
(13 sin leer) -
Menja't el coco! (30 sin leer)
-
Minervagigia (24 sin leer)
-
 No només filo
(61 sin leer)
No només filo
(61 sin leer) -
Orelles de burro (497 sin leer)
-
 SAPERE AUDERE
(490 sin leer)
SAPERE AUDERE
(490 sin leer) -
satiàgraha (25 sin leer)
-
 UN LUGAR PARA APRENDER FILOSOFÍA
(69 sin leer)
UN LUGAR PARA APRENDER FILOSOFÍA
(69 sin leer) -
 UNA CAIXA D´EINES PER PENSAR
(40 sin leer)
UNA CAIXA D´EINES PER PENSAR
(40 sin leer) -
 Vida de profesor
(177 sin leer)
Vida de profesor
(177 sin leer)
 (5 sin leer)
(5 sin leer)
-

 19:15
19:15 Exàmens de selectivitat 2018
» Comunitat Virtual de FilosofiaTeniu als documents adjunts els exàmens de selectivitat d’història de la filosofia de juny i setembre del 2018: juny 2018 setembre 2018 Podeu consultar les pautes de correcció també en els documents adjunts: juny 2018 correcció setembre 2018 correcció
-

9:54
Sobre preguntar i respondre
» Orelles de burroL’Olimpíada de filosofia de Catalunya ens fa el regal d’aquest còmic que ajuda a reflexionar sobre què es preguntar i què respondre...
4minuts de lectura
-

 7:30
7:30 Demostraciones sin palabras: suma de cuadrados
» Aprender a PensarEn matemáticas se ha acuñado la expresión “demostraciones sin palabras” para designar a diagramas, esquemas o dibujos que, aunque no son realmente demostraciones, nos ayudan a comprender por qué un teorema es cierto o encierran la idea de la verdadera demostración matemática. Además, las “demostraciones sin palabras” son siempre sugerentes, atractivas y todo un ejercicio de estímulo para el pensamiento.
Como comenta el matemático Roger B. Nelsen, autor de los dos libros Proofs without words publicados por la Mathematical Association of America, se fueron haciendo populares a raíz de su publicación, a partir de 1975, en revistas como Mathematics Magazine y The College Mathematical Journal, primero como imágenes de relleno entre artículos y posteriormente como secciones fijas.
Como ejemplo de demostración sin palabras veamos la prueba visual, e incluso táctil, de la fórmula de la suma de los cuadrados de los n primeros números naturales, publicada por Man-Keung Siu en 1984 en Mathematics Magazine. Realizaremos el esquema de esta demostración sin palabras para n = 4. Para empezar, consideramos tres copias de una cierta estructura geométrica, realizada con cubos del material Live Cube, que refleja la suma de los cuadrados de los 4 primeros números 12 + 22 + 32 + 42 = 1 + 4 + 9 + 16 cubos.
Después, se juntan las tres estructuras para formar una estructura compacta.

Los cubos de dicha estructura forman un ortoedro, es decir, un prisma recto de base rectangular, cuya base tiene n = 4 cubos de ancho y n + 1 = 5 cubos de largo, y con una altura de n = 4 cubos, luego n (n + 1) n = 80 cubos en total. Además en la parte de arriba del ortoedro hay 1 + 2 + 3 + 4 cubos más (en general, 1 + 2 + … + n cubos), que aún no habíamos contado.
Teniendo en cuenta la conocida fórmula de la suma de los n primeros números enteros naturales, 1 + 2 + … + n = n (n + 1) / 2, se obtiene, contando la cantidad de cubos que hay en la estructura de las dos formas explicadas, que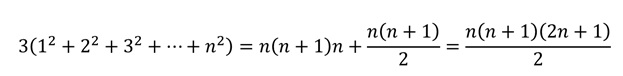
Si no conocíais la fórmula de la suma de los n primeros números enteros naturales, aquí os dejo una sugerente demostración sin palabras…
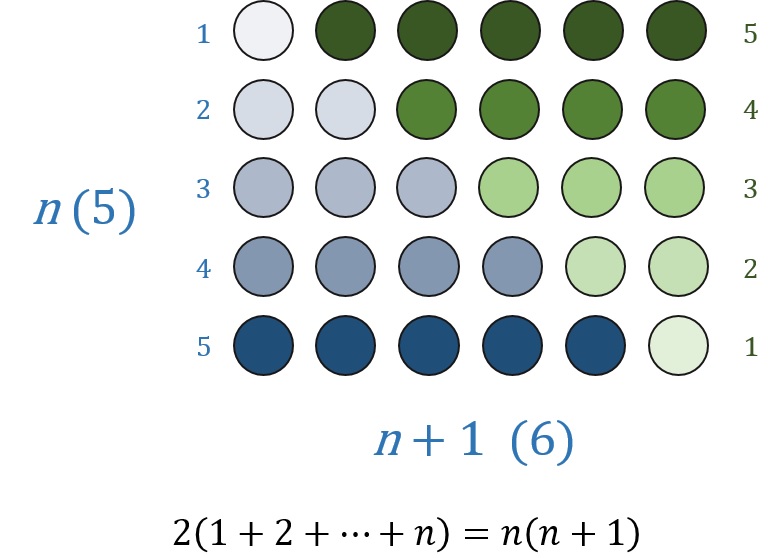
La entrada Demostraciones sin palabras: suma de cuadrados se publicó primero en Aprender a pensar.
-

 7:25
7:25 La importancia de tocar las mates
» Aprender a PensarPor Javier Bernabeu
Se habla mucho de la importancia de ir de lo concreto a lo abstracto. De que el aprendizaje de las matemáticas y sus símbolos deben partir de la manipulación de objetos concretos antes de llegar a la simbolización que representa dicha experiencia sensorial. ¡Los niños deben aprender mates partiendo de lo concreto! Y yo me pregunto, ¿solo los niños? Hagamos una pequeña prueba que nos permita comprobar hasta qué punto es importante partir de materiales concretos independientemente de ser niño o adulto. Y es que hay muchos adultos (entre los que me incluyo) que seguimos necesitando los materiales para poder resolver situaciones que, aparentemente, son sencillas incluso para un niño de 1.ºEP. A continuación, propondré un problema “sencillo” con una serie de preguntas. Trata de responder a cada pregunta con mente de adulto a la mayor velocidad que puedas… ¿Preparado? Ahí va:
Ana tiene 5 caramelos. Pepe tiene 4 caramelos
1.¿Cuántos caramelos tiene Ana?
2. ¿Cuántos caramelos tiene Pepe?
3. ¿Quién tiene menos caramelos, Ana o Pepe?
4. ¿Quién tiene más caramelos, Ana o Pepe?
5. ¿Cuántos caramelos más tiene Ana?
Pepe da uno de sus caramelos a Ana1.¿Quién tiene más ahora?
2. ¿Cuántos más?La respuesta a las 6 primeras preguntas se resuelven por comparación de cantidades sencillas. Sencillas para nosotros, adultos, que tenemos perfectamente interiorizado que el dibujo “5” representa una cantidad mayor que el dibujo “4”. La pregunta 7 requiere poner en marcha nuestro cerebro. Buscar una estrategia que nos permita resolver satisfactoriamente a la pregunta. La repuesta a la pregunta 7 es: “Ahora Ana tiene 3 caramelos más que Pepe”. ¿Respondiste 3 caramelos más o 2 caramelos más?
¿Por qué es importante manipular las mates desde que se es pequeño?
Resolvamos con manos y mente de niño: Una pieza representa un caramelo.
Una pieza representa un caramelo.
Comenzaremos estableciendo la unidad (caramelo en el problema de hoy).


¿Cuántos caramelos tiene Ana? ¿Cuántos tiene Pepe? ¿Quién tiene más? Con la representación anterior las preguntas de la 1 a la 4 se resuelven sin dificultad. En la pregunta 5, los niños suelen utilizar su dedo índice para señalar el hueco de la diferencia entre lo que tiene Pepe y lo que tiene Ana.
La historia del problema sigue así: “Pepe le da un caramelo a Ana”. La reacción típica de los niños es “¡Jooo qué morro, encima de que tiene más!” y es que la justicia es la justicia. En fin, la realidad es que ejecutan la acción pedida y le quitan un caramelo a Pepe para dárselo a Ana. Quedando su representación así:

La pregunta 6: “¿Quién tiene más?” es una pregunta ancla que es importante para que el alumno vuelva a analizar la situación que tiene delante de sus ojos. Ahora puede resolver la pregunta 7 desde el conteo o estableciendo “de súbito” la solución por comparación. “Ahora Ana tiene 3 caramelos más que Pepe”… ¡Qué morro! (vuelven a gritar). Benditos gritos esos que denotan razón y emoción.
Este problema que hemos analizado forma parte del Proyecto “Piensa Infinito. Metodología Singapur” de la editorial SM. Proyecto del que tengo la suerte de ser asesor pedagógico y formador. Este proyecto me ha brindado la oportunidad de visitar decenas de aulas para poder ver cómo se está implantando la metodología y aprender mucho, muchísimo de los profes y mucho, muchísimo de las reacciones de los niños… ¡Se les escucha pensar en voz alta! Muchas gracias a todos los profes que en el curso 17/18 nos abristeis las puertas de vuestras aulas y nos dejasteis aprender de vosotros, aprender con vosotros… ¡Y aprender de vuestros niños y con vuestros niños!
¿Respondiste 3 caramelos más o 2 caramelos más? Yo dije, 2 caramelos más.
La entrada La importancia de tocar las mates se publicó primero en Aprender a pensar.
-

 7:22
7:22 Divulgación de historia de las matemáticas
» Aprender a PensarPor Luis Español González
Equipo de Coordinación del GHM/RSMEHace poco más de un año este «Grupo especializado RSME» se presentó ante los interesados en la Biblioteca Estímulos Matemáticos de SM. Baste recordar que el GHM/RSME se dedica a difundir y potenciar el gusto y la curiosidad por, el estudio de y la investigación en historia de las matemáticas, y lo hace queriendo llegar a todas las personas que forman la comunidad matemática, entendida en el sentido más abierto posible. El Grupo tiene un equipo de coordinación de tres miembros que estamos accesibles por correo electrónico desde la página web de la RSME para cualquier contacto relacionado con la historia de las matemáticas.
Tenemos un interés especial en el papel que la historia juega en la educación matemática, tanto en la formación de los profesores cuanto en su posterior ejercicio profesional; también nos ocupamos de la presencia de la historia de las matemáticas en la divulgación de esta maravillosa ciencia. Invitamos, por ejemplo, a visitar la Sección de Historia de La Gaceta de la RSME para ver en ella artículos dedicados a diversos aspectos de la educación matemática, vinculados en la mayoría de los casos a biografías de destacados profesores.
Está accesible en el mismo portal digital el archivo completo de los números semanales del Boletín de la RSME, una publicación electrónica que toma el pulso a la actividad societaria con todo su rico y complejo mundo de relaciones institucionales, científicas y culturales.

Desde marzo de 2018, el GHM/RSME mantiene en el Boletín una sección llamada «Mat-Historia», rótulo que va acompañado de un pequeño icono alusivo a la famosa figura que ilustra la demostración del teorema de Pitágoras en la emblemática obra Elementos de Euclides.
El objetivo de la sección es mantener agrupadas la noticias de actualidad sobre historia de las matemáticas que van surgiendo y pueden tener interés para un público amplio. En principio, pensamos mantener un ritmo quincenal en las apariciones de Mat-Historia, pero el realismo ha impuesto una cadencia mensual, que nos lleva a la entrega nº 10 en diciembre de 2018.
Para quien tenga curiosidad por ver sus contenidos, indicamos que la sección Mat-Historia ha ido apareciendo en los Boletines nº 573, 575, 578, 581, 584, 588, 592, 596 y 601. Una de las actividades que se recogen es la celebración de aniversarios y otras efemérides asociadas a la historia de las matemáticas; así, este año se ha dado cuenta de la conmemoración del centenario de la muerte del gran matemático alemán George Cantor, artífice de la teoría de conjuntos, así como de las celebraciones en Colombia del 250 aniversario del nacimiento de Francisco José de Caldas, un ilustrado que tuvo un papel relevante en la ciencia y en la independencia de su país.

Otro de los objetivos del GHM es organizar reuniones científicas sobre historia de las matemáticas, en particular sesiones especiales en los congresos bienales de la RSME y en los mixtos con otras sociedades matemáticas. Acabamos de completar el programa de la que tendrá lugar durante el próximo Congreso Bienal RSME 2019, que se va a celebrar en Santander, acogido por la Universidad de Cantabria, del 4 al 8 de febrero; la mencionada Sesión Especial 15, Historia de las Matemáticas, ha sido programada para los día 7 y 8 de dicho mes.
La entrada Divulgación de historia de las matemáticas se publicó primero en Aprender a pensar.